Polyhedra used to illustrate bell ringing methods

by Fortran Friends

Although this is a site for learners, we have included some very technical stuff for those of you who are brilliant mathematicians and are fascinated by numbers. If you are not one of those people, don't be surprised and discouraged if you can't understand this. You can be a really good ringer and never even encounter Polyhedra!

Bells were originally just rung in order from the smallest (highest note, usually called the treble) to the biggest (lowest note, usually called the tenor), this is called rounds and is written out on a line, like this: 1 2 3 4 5 6
This sounds boring after a while, so about 400 years ago, change ringing was invented. Ways of changing the order were found and written down, with the next order on the next line, as in the column on the far left, which represents a method called 'A Plain Course of Bob Doubles'.
The leftmost column, is only 'B' or 'H', to show which row is handstroke and which a backstroke. The path of the treble is shown by a red line, that of bell 3 by a blue one. In this method there are 10 rows between where the treble starts in the first place and where it gets back to the first place, these 10 rows are called a lead. A black line is drawn under the line where this happens to make it easier to see, and a letter 'P' written at the end of the next line to show this is a Plain lead. The method continues in a predefined way until the bells return to rounds at the bottom, after 4 leads or 40 rows.

Since there are 5 changing bells if we want to ring the bells in all possible combinations of the 5 numbers, we must ring 120 rows (factorial 5, 5*4*3*2*1), making 12 lead-ends. The other changes and lead-ends are visited by changing the type of lead-end; the conductor calls "Bob" two rows before the treble gets back to the first place. This tells the ringers to change their order and then continue as before; when this happens a 'B' is printed at the lead end.

120 lines take much more space to write out than 40, so to make a more compact diagram leave out the lines where the bells are just 'plain hunting', look at the column on the right showing just the path of the bells, with each bell its own colour. The pattern only changes at the lead ends, so we can print just those rows, leaving the ringers to plain hunt in between.

We can leave out bell 6, because it is always in the same place and if we write out only lead ends we can also leave out bell 1 which is always first; look at the orange bars across the left diagram to see this.
A Plain course of Bob Doubles can be written as:
2 3 4 5
3 5 2 4
5 4 3 2
4 2 5 3
2 3 4 5
To show we were carrying on we could write more similar rows underneath but since these are always the same as those above, the numbers can be thought of as the corners of a square, shown at the right of the diagram below. The arrows show which way to move and the 'P' indicates a Plain lead.

If a 'Bob' is called we move along a line without an arrow on it, from a corner of the square to another square of Plain leads.

In the example of Bob Doubles the Plain course has four lead-ends giving the vertices of a square, with the direction of movement shown by the arrows; only two Bob lead-ends are needed to get back to the beginning so the polygon of these just form a line along which you can move in either direction, so these lines have no arrows. Because there are 24 lead-ends in all there must be 6 such squares joined by Bob lines. The Bob lines join up with Plain lead squares to form hexagons like this:
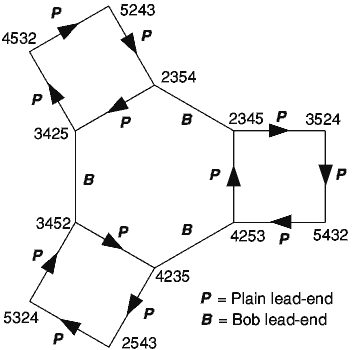
hexagon+square
This figure shows part of what is possible with Bob Doubles - only three of the six squares of Plain leads are shown. There are eight hexagons altogether made from alternating Plain and Bob lead-ends.

Folding up the complete plan of squares and hexagons makes a 3D solid (called a Truncated Octahedron by mathematicians), where the 24 possible lead-ends are arranged at the vertices of a polyhedron and the edges of the polyhedron show how to get from one lead-end to the next. If you visit all the vertices in turn obeying the directions given by the arrows you will have completed all the possible combinations on 5 bells ringing Bob Doubles.

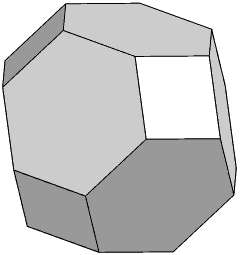
A Truncated Octahedron

This is the plain model without the bell sequences or arrows printed on it.
Similarly the Grandsire Doubles method can be represented by a Truncated Tetrahedron.
You can download templates with instructions to make both these models either as zipped Draw files (10K) or as a PDF file (10K). These polyhedra have the bell numbers for that lead printed on them, and arrows drawn along the edges which are plain leads.
You can find out more about polyhedra by looking at some of our other pages.
Web address: http://fortran.orpheusweb.co.uk/Bells/